|
One of the key values used to describe the orbit of one body around another, sometimes spelt 'semimajor axis' and represented in calculations by the letter a. The semi-major axis is fundamental to defining the distance of a body in an elliptical orbit body from the primary focus of that orbit.
Definition
For a perfectly circular orbit, the distance between the two objects would be simple to define: it would be the radius of the orbit's circle. In reality, orbits are not perfectly circular: instead they follow an elliptical path, with the orbited body lying at one of the two foci of the ellipse. This means that the distance between the two bodies is constantly changing, so that we need a base value in order to calculate the actual orbital distance at any given time.
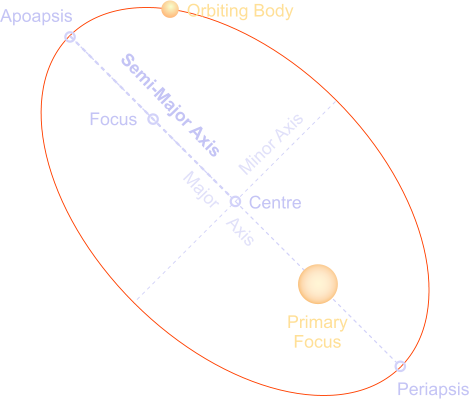

An ellipse has two axes, a major axis and a minor axis. The major axis is the longest diameter of the ellipse measured through its centre and both of its foci (while the minor axis is the shortest diameter, perpendicular to the major axis). The semi-major axis is half the length of the major axis, a radius of the ellipse running from the centre, through one of the foci, to the edge. It is thus the longest possible radius for the orbital ellipse. This semi-major axis provides a baseline value for calculating the distances of orbiting objects from their primary body.
Application
The semi-major axis gives a useful shorthand for describing the distance of one object to another (sometimes described as their 'average' distance though, strictly speaking, calculating an average distance is a little more involved). For example, the semi-major axis of Earth in its orbit around the Sun is 149,598,023 km (or 92,955,902 miles), a value essentially equivalent to one Astronomical Unit or 'AU'. In reality, Earth's orbit is slightly elliptical, so its actual distance from the Sun can vary up to some 2,500,000 km from this base value.
Though measured along the longest axis of the orbital ellipse, the semi-major axis does not represent the largest possible distance between two orbiting bodies. This is because it is measured from the abstract centre of the ellipse, whereas the object being orbited will actually lie at one of the ellipse's foci, potentially some distance from its central point.
The actual extreme distances depend on the relative positions of the orbiting body and its orbital focus, and they apply when the body reaches one or other end of the long axis of its orbital ellipse. At the end closest to its orbital focus, it reaches its nearest approach or periapsis, while at the opposite end of the major axis, it finds itself at its greatest possible distance or apoapsis.
The more eccentric the orbit, the more extreme these values can be, and the more widely removed from the underlying semi-major axis. To take an extreme example, Halley's Comet has a semi-major axis of 17.8 AU. If it happened to follow a circular orbit around the Sun, that distance would place it a little within the orbit of Uranus. However, its true orbit is very far from circular, with an eccentricity of 0.97 meaning that it follows an extremely long, narrow elliptical path with the Sun at a focus near one end of the major axis.
When the comet reaches the outer end of its elliptical orbit, it can travel as far as 35 AU from the Sun - some considerable distance beyond Neptune's orbit. At the other extreme of its path, it reaches the inner end of its major axis and arrives at a periapsis point (or perihelion* in this case) of just 0.59 AU from the Sun, well within the orbit of Venus.
This extreme example shows that knowing the semi-major axis alone does not always help to visualise an object's distance from its primary. However, when combined with the orbital eccentricity (the degree of ellipticality) it can be used to describe typical orbits with great precision.
* Periapsis (or periapse) is the general term for the closest orbital approach of any two bodies. For certain very common cases, such as the Sun or Earth, specialised terms are used. The closest orbital approach of any body to the Sun is its perihelion, and for an object orbiting Earth, the equivalent is its perigee.
|